Leren rekenen in groep 3 met de lusabacus

In groep 3 van het Nederlandse rekenonderwijs speelt het rekenrek een belangrijke rol. Dit is het houten rekje met de horizontale staven, waaraan rode en witte kralen zijn bevestigd. Het rekenrek is bedoeld om het getalbegrip bij de leerlingen te versterken en om eenvoudige rekenbewerkingen op te maken. Hoewel het daarvoor op het eerste gezicht prima geschikt lijkt, duiken er toch een aantal problemen op. Daarom raad ik aan om een lusabacus te gebruiken in de rekenlessen in groep 3. Deze bestaat uit verticale staven met kralen die per tien zijn geordend op kleur. In dit artikel bespreek ik de werking van beide leermiddelen en laat ik zien waarom een lusabacus een betere didactische keuze is.

Op een rekenrek kunnen eenvoudige rekenbewerkingen tot en met 20 worden uitgevoerd. De kralen zijn in rood en wit per vijf geordend. Deze vijfstructuur sluit aan op de vijf vingers aan iedere hand. Hiermee maken leerlingen de stap van het eigen lijf naar rekenmateriaal dat hoeveelheden representeert. De tienstructuur wordt zichtbaar met de tien kralen op iedere staaf of door de tien rode kralen links en tien witte rechts.

Er zijn hierbij een aantal kanttekeningen te plaatsen. Allereerst draagt de focus op de vijfstructuur van de vingers niet bij aan het leren doorzien van de tienstructuur van getallen. Nog belangrijker is dat de horizontale plaatsing van de staven niet aansluit op het verticale positiesysteem van getallen. Daarnaast duiken er problemen op bij het maken van sommen.

Laat ik dit illustreren aan de hand van de optelling 8 + 6 = ... Om een bewerking te starten moet het rekenrek eerst worden leeggemaakt. De meeste rekenmethodes laten de kralen naar rechts schuiven en benoemen dit als ‘het rekenrek in rust’. Alle kralen blijven echter zichtbaar en dit bemoeilijkt het richten van de aandacht op de kralen waarmee de bewerking moet worden uitgevoerd. Ook vraagt het een extra denkstap van de leerlingen: welke kant moeten de kralen ook alweer op?

Alle kralen worden naar rechts geschoven om te kunnen starten met het uitrekenen van 8 + 6 = … We schuiven eerst 8 kralen naar links, en schuiven er 1, 2 kralen bij. Hiermee maken we het tiental vol op de bovenste staaf en tellen dan op de onderste staaf verder: plus 3, 4, 5 en 6. We kunnen nu snel het antwoord aflezen: 10 kralen boven en 4 kralen onder. Het antwoord is dus 14.

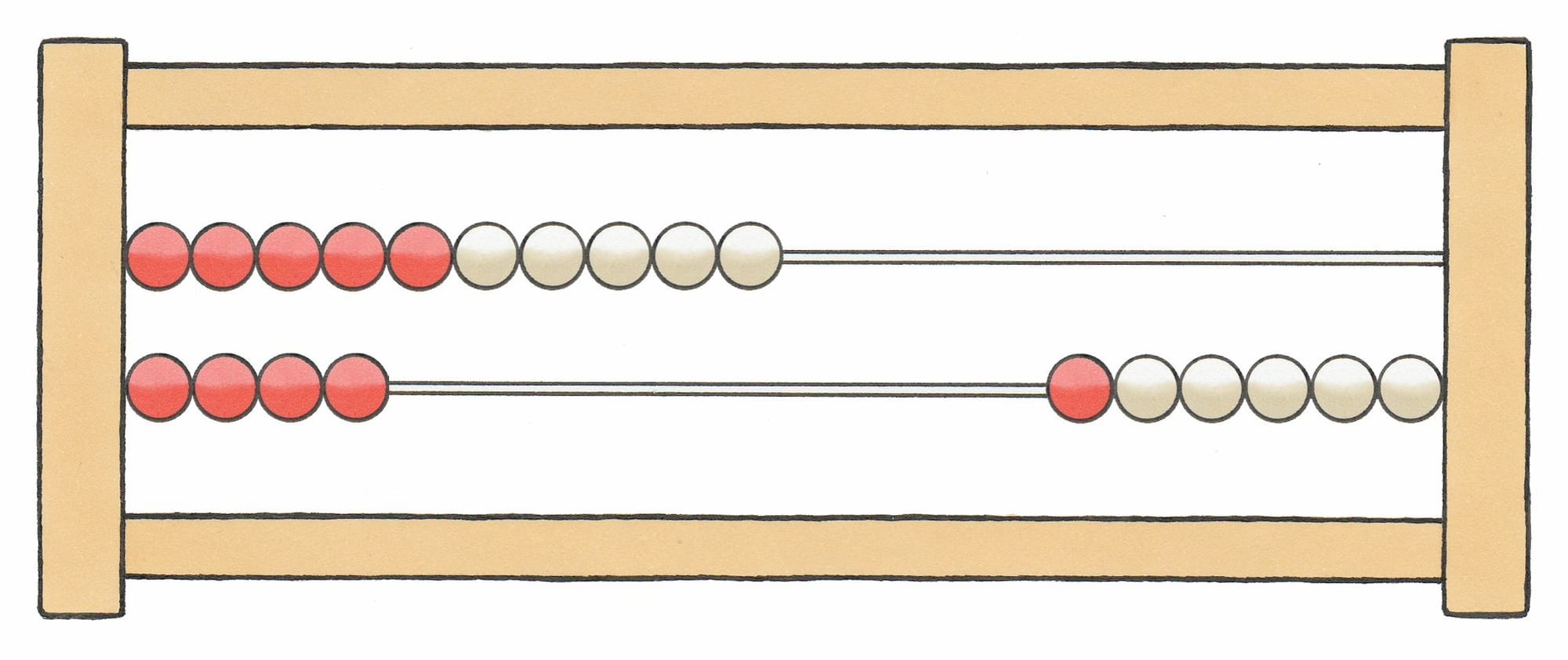
Toch kan er verwarring ontstaan. Doordat de 6 ongebruikte kralen rechtsonder ook zichtbaar zijn, bestaat de kans dat leerlingen deze tellen en als antwoord beschouwen. En wat is de functie van de kleuren? Er zijn 9 rode kralen en 5 witte in het antwoord. Moeten die weer worden opgeteld tot 14? Dat leidt af van de tienstructuur van de bovenste staaf.

Verder staan de rode kralen links en de witte rechts. Wat is de betekenis daarvan? Is het antwoord soms 95? In een getal staan de tientallen namelijk links en de eenheden rechts, maar op een rekenrek is dit niet zo. Kortom: het rekenrek laat volop ruimte voor misconcepties bij de leerlingen.

Tot slot is er nog de gemiste kans van het abstract leren denken. Op een rekenrek wordt namelijk altijd gerekend met de echte waarden: dus tien kralen blijven tien kralen. Ze kunnen niet worden ingewisseld voor een kraal die een tiental vertegenwoordigt. Hiermee is het onmogelijk om leerlingen duidelijk te maken dat de verschillende posities in een getal verschillende waarden vertegenwoordigen.

Zo blijven leerlingen hangen in hun eigen kleine leefwereld van het tellen van werkelijke hoeveelheden kralen. In plaats daarvan moeten ze worden meegenomen naar de rekenwereld waar abstract denken en redeneren worden gestimuleerd, doordat een kraal ook een tiental kan vertegenwoordigen. Dat is een belangrijk leerdoel van groep 3.

Getalstructuur

Getallen zijn opgebouwd uit cijfers, waarbij de positie de waarde van het cijfer bepaalt: honderdtallen, tientallen en eenheden. Dankzij deze getalstructuur met positiewaarden kunnen we met een beperkt aantal cijfers, namelijk 0 tot en met 9, eenvoudig alle denkbare getallen schrijven en vlot lezen.

In groep 3 leren de leerlingen bijvoorbeeld het getal 14 schrijven, en ermee rekenen. Ze moeten dan begrijpen dat de 1 staat voor één tiental en de 4 voor vier eenheden.

Om leerlingen een goed begrip bij te brengen van de structuur van getallen moeten we helder uitleggen hoe deze zijn opgebouwd. De lusabacus is hiervoor uitermate geschikt, omdat de verticale staven de waardeposities in een getal visualiseren.

Lusabacus

Laten we de eerdere optelling 8 + 6 = … nu ook eens op de lusabacus maken. De lusabacus is leeg: alle kralen bevinden zich achter het houten tussenschot. Leerlingen worden daardoor niet afgeleid door kralen die niet worden gebruikt. De aandacht kan volledig worden gericht op de bewerking en de kralen die daarvoor nodig zijn. De benodigde kralen worden opgezet: eerst 8 kralen en daarna doen we er 6 bij.

De kralen zijn door middel van kleuren geordend in groepjes van 10, waardoor de tienstructuur van getallen wordt benadrukt en verduidelijkt. Ook is het antwoord snel af te lezen: 10 rode kralen en 4 gele zijn samen 14 kralen.

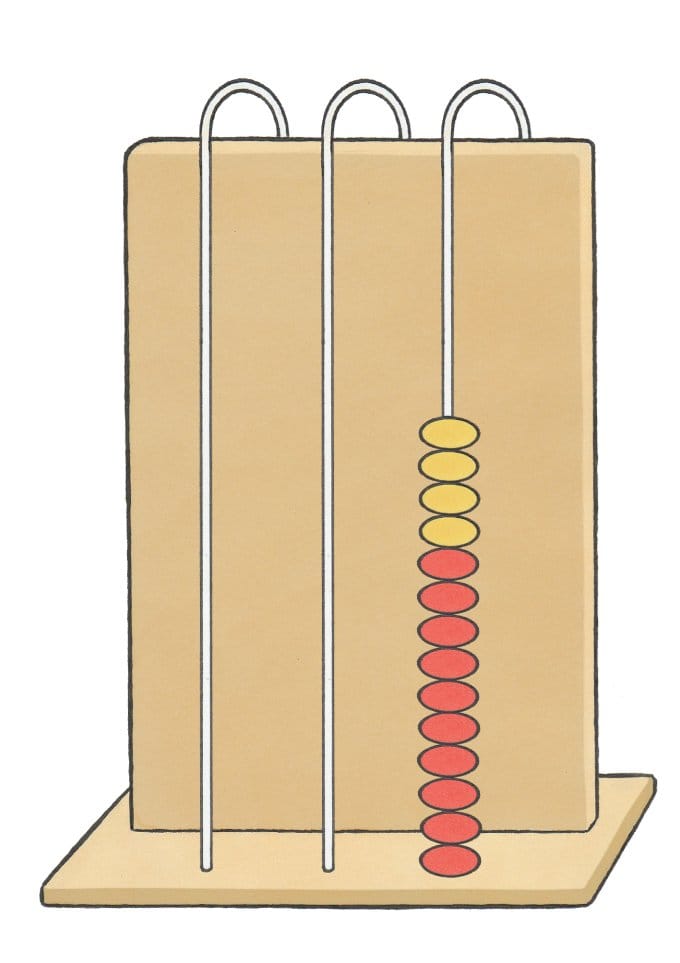
Maar de werkelijke kracht van de lusabacus schuilt in de positiewaarden en het kunnen inwisselen van tien eenheden voor een tiental. Als de optelling 8 + 6 = 14 is voltooid, dan zien leerlingen dat er een vol tiental is (10 rode kralen). Tien eenheden worden ingewisseld voor één tiental. Leerlingen ervaren hiermee op concrete wijze dat één tiental een waarde van tien eenheden vertegenwoordigt. Door de kralen op de lusabacus fysiek te verplaatsen en in te wisselen, ontstaat er een dieper inzicht in de positiewaarden en snappen leerlingen beter waarom het getal 14 bestaat uit de cijfers 1 en 4.

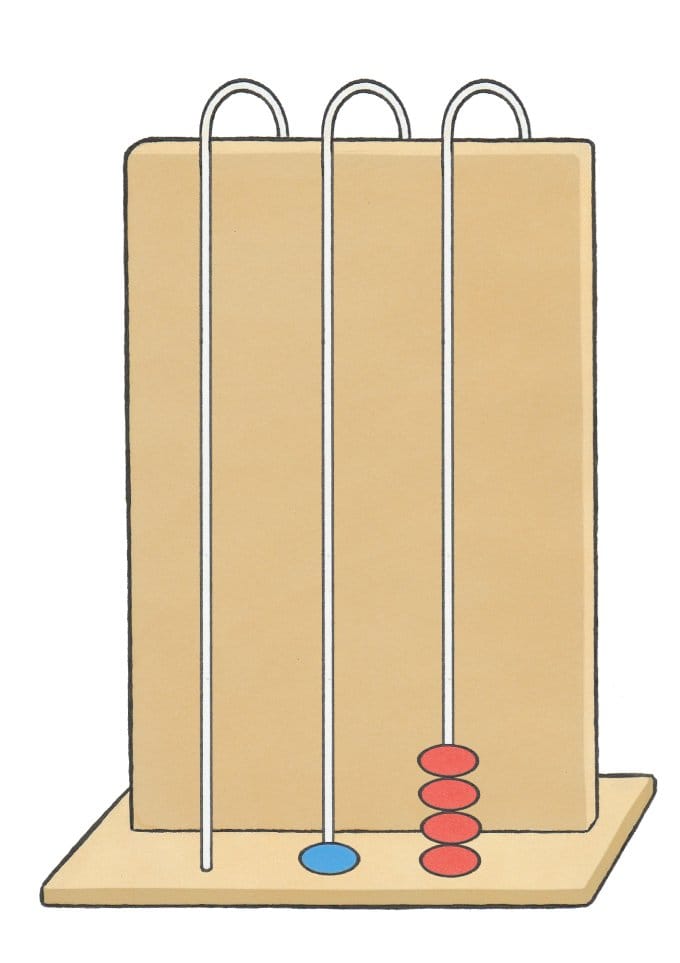
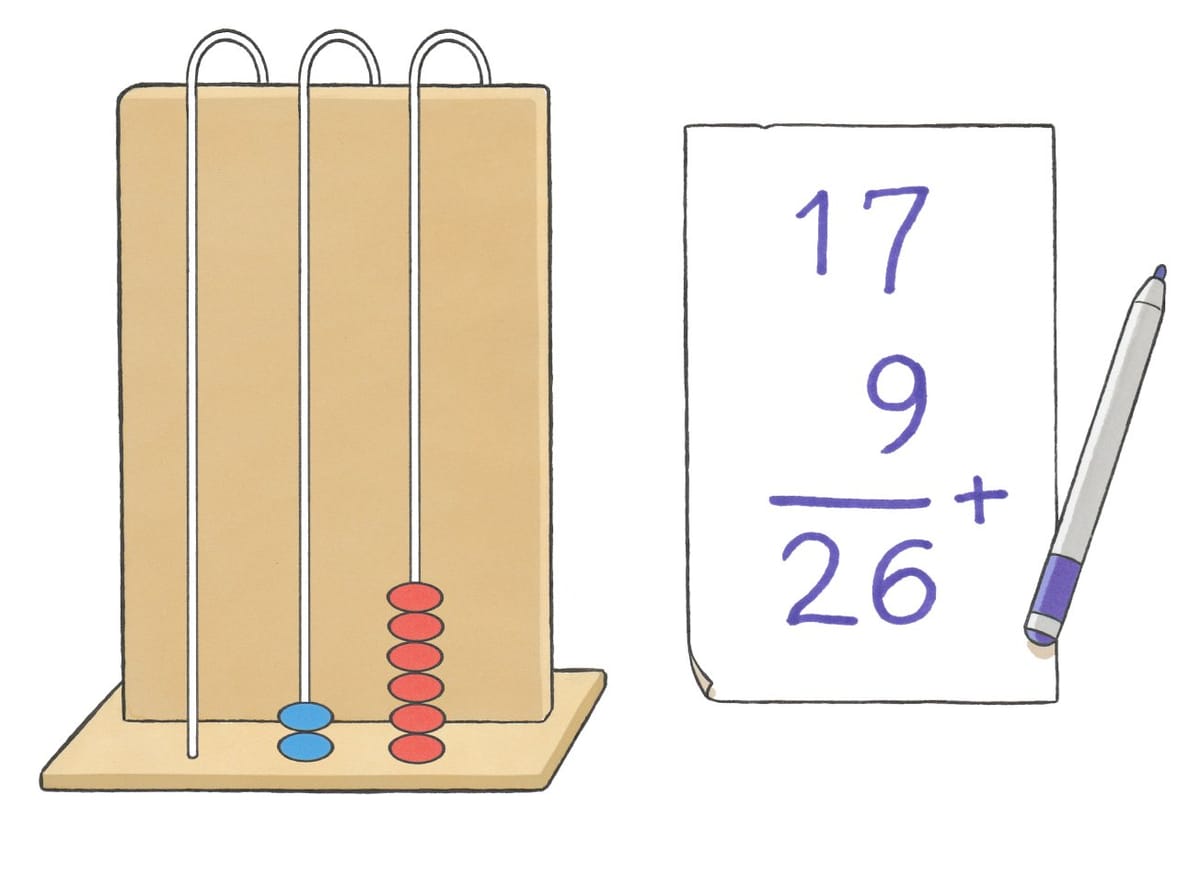
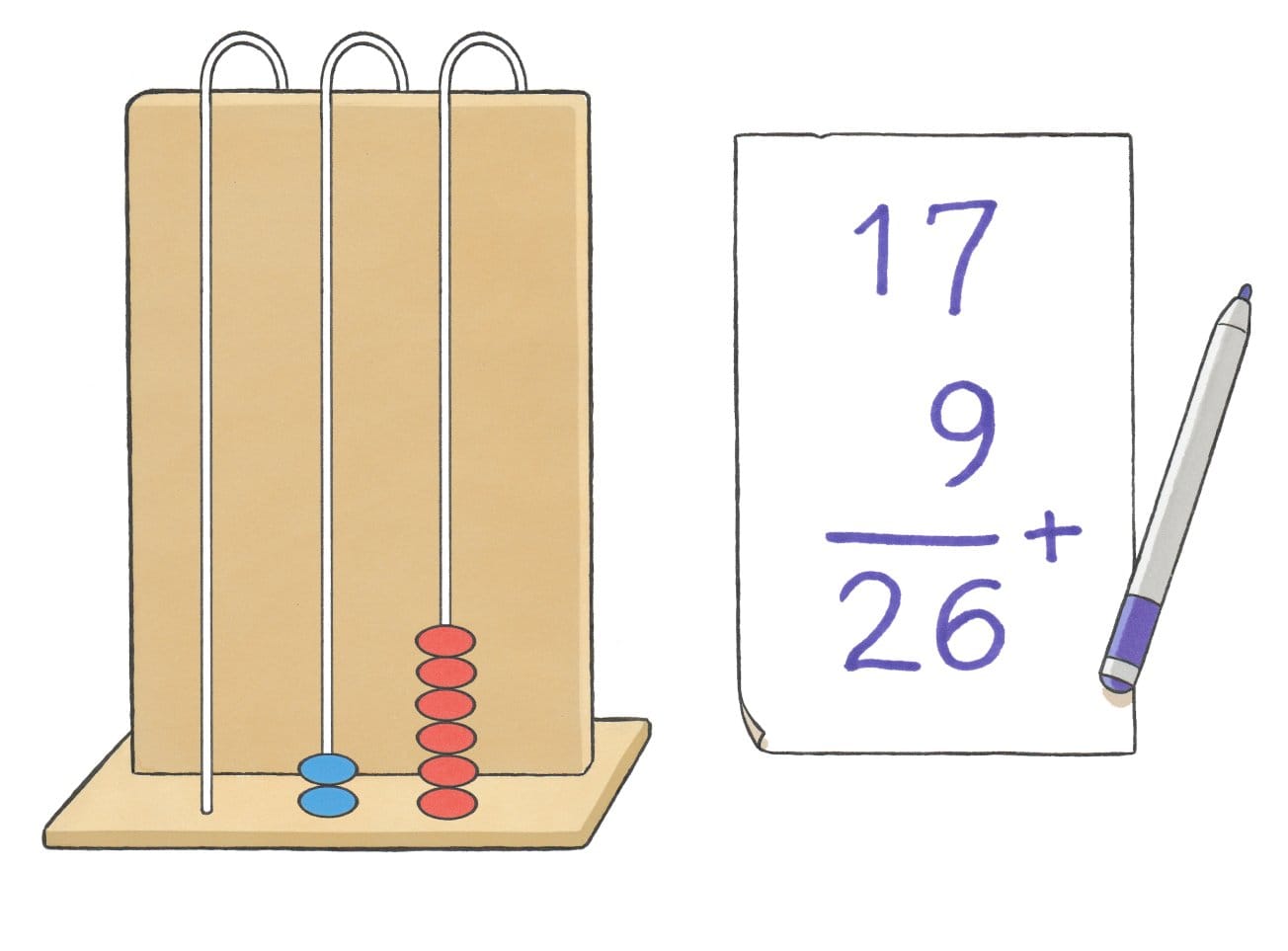
In de eerste helft van groep 3 worden op de lusabacus sommen tot 10 (zoals 5 + 2 = 7) gemaakt op alleen de rechter staaf. De sprong over het tiental (zoals 8 + 6 = 14) wordt in de tweede helft van groep 3 onderwezen. De laatste weken van groep 3 wordt er ook over het tweede tiental gerekend, zoals 17 + 9 = 26.

Een lusabacus is een krachtig didactisch hulpmiddel om het conceptueel begrip van getallen en bewerkingen te vergroten en vergemakkelijkt de stap naar het abstract rekenen met cijfers en symbolen op papier.

Doorgaande lijn

In groep 1 en 2 ontwikkelen leerlingen getalbegrip en leren ze dat hoeveelheden tot 20, zoals vingers en kralen, worden gerepresenteerd door getallen. Hier past het rekenrek goed bij. Vervolgens krijgen ze in groep 3 inzicht in getalstructuur en leren ze dat getallen zijn opgebouwd uit cijfers die verschillende waarden vertegenwoordigen, afhankelijk van hun positie in het getal. Daarvoor is de lusabacus meer geschikt. Ze leren optellen en aftrekken over het eerste en tweede tiental.

Als vervolgens in groep 4 tot 100 moet worden gerekend met lenen en inwisselen (54 – 37 = … en 48 + 26 = …), dan kan dit ook op de lusabacus worden uitgevoerd. Doordat er niet hoeft te worden gewisseld van materiaal, wordt met de lusabacus een doorgaande lijn gerealiseerd met consistent didactisch materiaal dat het inzicht en begrip in de getalstructuur en van de rekenbewerkingen versterkt.

Tot slot

De lusabacus is een goede didactische keuze, omdat deze goed aansluit op de structuur van getallen en er eind groep 3 ook sommen tot 30 op kunnen worden uitgerekend. Het abstract denken wordt ermee gestimuleerd én er hoeft niet van materiaal te worden gewisseld in hogere leerjaren. Hierdoor ontstaat er bij de leerlingen dieper begrip en leren ze vlot en foutloos sommen uitrekenen.